🐟 생선구분하기_K최근접이웃모델
데이터 처리
- 빙어와 도미 데이터
- 생선의 종류를 분류(구분)하기 위한 모델 생성을 위해 독립변수와 종속변수로 데이터를 가공해야함
- 독립변수(x) : 길이, 무게
- 종속변수(y) : 생선종류(빙어 또는 도미)
🐟 라이브러리
import matplotlib.pyplot as plt
🐟 데이터 불러오기
# - 도미 길이(cm)
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0,
30.0, 30.7, 31.0, 31.0, 31.5, 32.0, 32.0, 32.0,
33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5,
39.5, 41.0, 41.0]
# - 도미 무게(g)
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0,
390.0, 450.0, 500.0, 475.0, 500.0, 500.0, 340.0,
600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0,
685.0, 620.0, 680.0, 700.0, 725.0, 720.0, 714.0,
850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
# - 빙어 길이(cm)
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
# - 빙어 무게(g)
smelt_weight= [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
데이터 분포 확인하기
🐟 도미 데이터 산점도 그래프 그리기 : scatter()
- x축에는 길이, y축에는 무게
- 길이가 길어질수록, 무게가 커질까?
plt.scatter (bream_length, bream_weight)
plt.xlabel("length")
plt.ylabel("weight")
plt.show()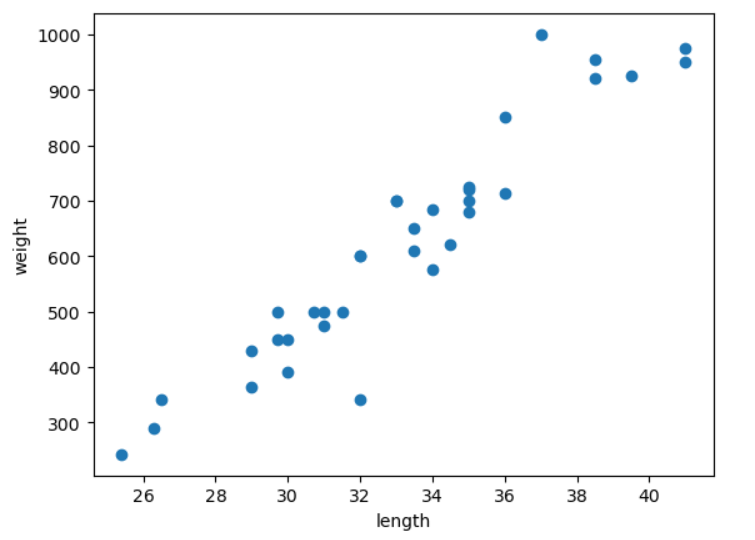
해석
- 길이가 길어질수록 무게가 커지는 특징을 가지고 있음
- 분포의 방향은 양(+)의 상관관계를 나타내고 있음
- 양(+)의 상관관계를 우상향 분포라고 칭함
- 우상향 분포를 선형 형태라고도 칭함
- 모델을 분석하는 입장에서는 선형 형태를 나타낸다고 해석하 며, 선형형태에 대한 분석은 회귀분석을 사용한다.
- 선형형태 = 회귀분석
- 도미와 생선을 구분하기 위한 모델 사용
- 구분 = 분류
- 분류 모델을 이용해서 진행
- 알고 있는 정보 : 길이, 무게, 생선 이름
🐟 빙어 데이터 산점도 그래프 그리기 : scatter()
- x축에는 길이, y축에는 무게
- 길이가 길어질수록, 무게가 커질까?
plt.scatter(smelt_length, smelt_weight)
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
🐟 도미와 빙어의 분포 확인하기(산점도 그리기)
plt.scatter (bream_length, bream_weight, c="red", label="bream")
plt.scatter(smelt_length, smelt_weight, c="blue", label="smelt")
plt.xlabel("length")
plt.ylabel("weight")
plt.legend()
plt.show()
도미와 빙어 비교 해석
- 도미와 빙어 모두 우상향 분포를 나타내고 있음
- 도미 데이터는 경사가 급한 반면, 빙어 데이터는 경사가 완만하게 분포되어 있음
생선 분류하기(도미와 빙어 구분하기)
🐟 회귀분석의 분류모델을 사용
- K최근접이웃 모델 사용
- KNN : K최근접이웃모델
- 머신러닝에서 가장 간단한 모델
- 비교용으로 주로 사용되는 모델(실제 사용되기에는 성능이 약한 모델)
- KNN 처리 방법 : 예측하고자 하는 값과 가장 가까운 이웃 갯수의 비율(또는 평균)을 이용하여, 비율이 가장 많은 쪽(다수결의 원칙을 따름)의 값으로 판단하는 방식
🐟 데이터 통합하기
- 도미와 빙어 데이터를 각각 하나의 길이와 무게 데이터로 통합하기
# - 길이(length)
length = bream_length + smelt_length
# - 무게(weight)
weight = bream_weight + smelt_weight
len(length), len(weight)
🐟 데이터를 2차원 형식으로 변형
- 이전의 length, weight는 1차원

- 머신러닝에서 사용하는 데이터 차원은 2차원
- 독립변수(길이와 무게) → 독립변수는 2차원 데이터 형태
- 종속변수(생선 이름) → 종속변수는 1차원 데이터 형태
🐟 독립변수(길이와 무게) 생성하기
- 2차원으로 생성 : [[길이, 무게], [길이, 무게], ...]
fish_data = [[l, w]for l, w in zip(length, weight)]
print(fish_data)
len(fish_data)
🐟 종속변수(생선이름) 생성하기
- 1차원으로 생성 : ["도미", "도미", ..., "빙어"]
- 종속변수로 사용하는 데이터 형태 : 정수형을 주로 사용
- 범주 값의 갯수에 따라 : 0 ~ n 값을 사용
- 이진분류 : 0 또는 1 사용
- 다중분류 : 0 ~ n개 사용
- (이진분류)도미 : 빙어 = 1 : 0
- 이진분류에서는 찾고자 하는 값을 1로 정의하는 것이 일반적 개념
- 다만, 어떤 값을 사용하여도 무관
fish_target = [1]*35 + [0]*14
print(fish_target)
len(fish_target)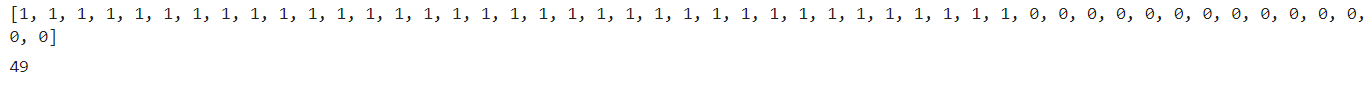
모델 생성하기
from sklearn.neighbors import KNeighborsClassifier
🐟 분류모델(클래스) 생성시키기
kn = KNeighborsClassifier()
kn
모델 훈련(학습) 시키기
- KNN은 지도학습 모델 : 독립변수와 종속변수 모두 사용
- 훈련(학습) 시키는 함수 : fit()
kn.fit(fish_data, fish_target)
모델 정확도 확인하기
🐟 모델 훈련(학습)이 잘 되었는지 확인하는 절차
- score() 정확도 확인하는 함수
- 첫번째 값 : 예측하고자하는 값
- 두번째 값 : 실제 정답
- score()함수는 첫번째 값만 이용해서 훈련모델의 패턴에 적용하여 예측결과를 추출
- 추출된 예측결과와 두번째 값(실제 정답)과 비교하여 얼마나 잘 맞추었는지 비교
kn.score(fish_data, fish_target)
해석
분류에서의 정확도 : 0 ~ 1 사이의 값이 출력됨
0 ~ 1 : 0% ~ 100%의 정확도를 의미함
💡(훈련에 사용한 데이터를 이용해서) 정확도를 확인 했을 때 1.0의 정확도는 과대적합이라고 칭함
🐟 예측 : 임의값으로 예측하기
- 예측 : predict() 함수 사용
- 예측 시에는 정답은 알려주지 않고, 문제만 넣어준다
- 즉, 문제는 독립변수에 속하며, 2차원 데이터를 사용해야 한다.
- 훈련에 사용된 독립변수 형태 그대로 사용해야 한다. await
kn.predict([[30, 600]])
1 = 도미로 예측
🐟 산점도 그리기
plt.scatter (bream_length, bream_weight, c="red", label="bream")
plt.scatter(smelt_length, smelt_weight, c="blue", label="smelt")
plt.scatter(30, 600,marker='^', c="green", label="pred")
plt.xlabel("length")
plt.ylabel("weight")
plt.legend()
plt.show()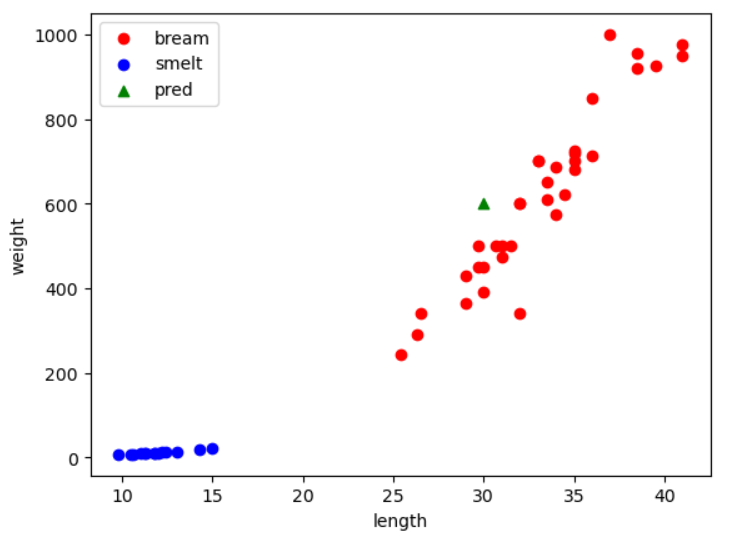
해석
- 임의 예측 데이터가 분포한 위치를 통해서 시각적으로 확인가능
- 모델(클래스)이 사용하는 기본 이웃의 값은 5개를 기준으로 한다.
하이퍼파라메터 튜닝
🐟 하이퍼파라메터 튜닝
- 모델 성능을 향상시키기 위한 방법
- 과대적합 또는 과소적합이 일어난 경우 튜닝 진행
🐟 하이퍼파라메터
- 모델(클래스)의 속성 중에 사람이 직접 값을 지정해 주어야하는 변수들을 통칭 한다.
🐟 KNN 모델 생성하기
- n_neighbors : 이웃의 갯수(하이퍼파라메터 속성)
kn20 = KNeighborsClassifier(n_neighbors=20)
🐟 모델 훈련시키기
kn20.fit(fish_data, fish_target)
🐟 훈련 정확도 확인하기
kn20.score(fish_data, fish_target)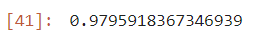
매우 좋은 성능을 보이는 모델이다라고 표현
🐟 예측하기
kn20.predict([[30, 600]])
🐟 튜닝 계속 진행
- 방법1 : 이미 훈련은 되어있고 이웃의 갯수만 바꿔서 진행
# 1
kn20.n_neighbors = 40
kn20.score(fish_data, fish_target)
# 2
kn20.n_neighbors = 15
kn20.score(fish_data, fish_target)
# 3
kn20.n_neighbors = 5
kn20.score(fish_data, fish_target)
- 방법2 : 반복문 사용하여 1보다 작은 가장 좋은 정확도일 때의 이웃의 갯수 찾기
### 모델(클래스 생성)
kn = KNeighborsClassifier()
### 훈련시키기
kn.fit(fish_data, fish_target)
### 정확도가 가장 높을 떄의 이웃의 갯수를 담을 변수
nCnt = 0
###정확도가 가장 높을때의 값을 담을 변수
nScore = 0
# - 반복문 사용 : 범위는 3 ~ 전체 데이터 갯수
for n in range(3, len(fish_data), 2):
kn20.n_neighbors = n
score = kn20.score(fish_data, fish_target)
print(f"{n} / {score}")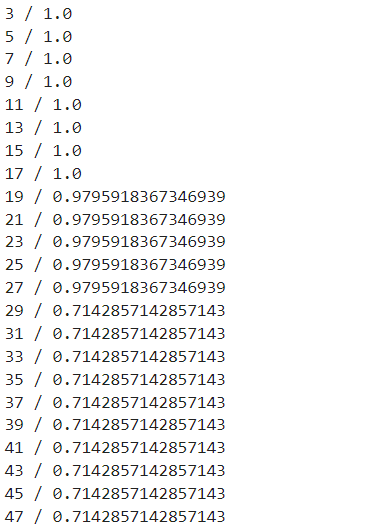
19일 때 가장 높은 정확도를 가짐
동일한 정확도일 때 이웃 갯수가 많을수록 PC과부하
그러므로 가장 갯수가 적은 19를 선택
for n in range(3, len(fish_data), 2):
kn20.n_neighbors = n
score = kn20.score(fish_data, fish_target)
#print(f"{n} / {score}")
### 1보다 작은 정확도인 경우
if score < 1 :
### nScore의 값이 score보다 작은 경우 담기
if nScore < score :
nScore = score
nCnt = n
print(f"nCnt = {nCnt} / nScore = {nScore}")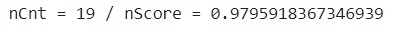
해석 : 모델의 성능이 가장 좋은 시점의 이웃의 갯수를 추출하기 위한 하이퍼파리메터 튜닝 결과, 이웃의 갯수 19개를 사용하였을 때가장 좋은 성능을 발휘하는 것으로 확인 됨
🐟 최종 모델 검증
kn.n_neighbors = nCnt
kn.score(fish_data, fish_target)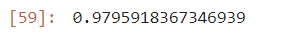
kn.predict([[10, 30]])
'Digital Boot > 인공지능' 카테고리의 다른 글
| [인공지능][ML] Machine Learning - 분류모델 / 앙상블모델 / 배깅 / 부스팅 / 랜덤포레스트 (0) | 2023.12.26 |
|---|---|
| [인공지능][ML] Machine Learning - 선형회귀모델 / 다항회귀모델 / 다중회귀모델 (0) | 2023.12.21 |
| [인공지능][ML] Machine Learning - KNN 회귀모델 / 평균절대오차(MAE) (0) | 2023.12.21 |
| [인공지능][ML] Machine Learning - 훈련 및 테스트 데이터 분류하기 / 정규화 (3) | 2023.12.20 |
| [인공지능] Machine Learning - 개요 / 실습 (3) | 2023.12.19 |